![]()
Inductive Solutions, Inc.
Home
Products and Services Bibliography and White Papers
Sample Course: An Introduction to Risk
Management
Software Products
Consulting
Recommended Books
Free Downloads
An introduction to Risk Management
- Uncertainty and Risk Assessment: Background
- Model Risk, Operational Risk, Compliance Risk
- Financial Risk Assessment
- A Simple Model of Returns
- Value at Risk
- A Simple Model of Portfolio Returns
- Insurance, Hedging, and Replicating Portfolios
- Credit Risk vs. Market Risk
- Models for Interest Rates: Spot and Forward Rates
- Integrated Financial Risk Assessment
- Afterward: Risk Quotes
"If you can't measure it then you can't manage it," is a common saying that justifies many quantitative methods. The following pages provide an introduction to risk assessment and risk management from a quantitative perspective, with a focus on financial applications.
In some sense, risk is a statistical description of danger — an attribute that rational beings seek to minimize. Predicting natural, political, and financial disasters are difficult, to say the least, unless one is as pessimistic as Pascal. His point is that since disasters happen so often, then over a long time horizon, any indicator will predict one.
On the other hand, a description of risk purely in terms of mathematical expectation is misleading, since this sense of risk replaces the risk of an individual with the risk of an average. In other words, the probability that somebody wins the New York Lottery is 100%, but the likelihood that you will win the lottery is very small. From a financial perspective, this is what can get investors into trouble.
Over the past years, we have seen how the risks associated with currency devaluation, interest rate movements, leverage in derivative markets, and "the irrational exuberance" over some equities led to near-disasters for some market participants, investors, and governments. Some of these situations could have been avoided if the dangers associated with these instruments were made more comprehensible. One of the responsibilities of risk professionals is to help make risk assessment understandable and measurable.
Uncertainty and Risk Assessment: Background
In an uncertain world, events may not turn out the way they are supposed to. Decisions that seemed correct at one time may, on retrospect, have been wrong because of the way actual events played out. The mistake was on relying on an incorrect model of the world at the time the decision was made.
Risk assessment is concerned with understanding the effects of adverse events on a decision, plan, or value of an asset: an assessment not of what did happen in the past but of what could happen in the future. If we can understand how adverse events will change the world then we can insure (or hedge) against them by preparing for that "rainy day." This one of the goals of risk management.
From a quantitative perspective, risk assessment requires a mathematical model of the world consisting of several input factors that are related to a measurable output. A natural setting for such a model is in the realm of probability and statistics. If we assume that we know the underlying probability distribution on how events will play out — and the precise relationship of the input factors to the output results — then risk assessment is reduced to estimating the likelihood of these adverse events occurring over a given time horizon. Once the model is in place, insurance costs can be calculated.
Model Risk, Operational Risk, Compliance Risk
Unfortunately, the only way to estimate a future probability distribution is to estimate a past probability distribution (a statistical problem) and hope that the past and future distributions are not too much different (the so-called stationary assumption). This assumption is reasonable in some domains (e.g., identifying a signal from natural noise in the domain of radio communication) but not reasonable in other domains (e.g., identifying a profitable security in an emerging market). Moreover, the mathematical model may have insufficient factors, the wrong factors, or the wrong functional relationship. This induces a risk in using the model per se, called model risk.
Model risk is seen when different models react differently to different events, and produce different answers (which may or may not be correct or "good enough"). Many problems associated with model risk are due to incompleteness inherent in any model — there is no such thing as a perfect model:
- The models may be based on an incomplete theory or an inadequate theoretical approximation.
- The model inputs may be incomplete because some important factors have not been included.
- The model outputs may be incomplete because they require additional interpretation. (This is especially true for models with uncertain outcomes, like a weather forecast or an economic assessment.)
Other problems associated with model risk can be traced to the statistical methodology used to compute model parameters. This operational risk includes parameter estimation risk: the differences in results due to estimating the model parameters in different ways.
For example, suppose we want to estimate the likelihood of a hit the next time a ball player comes up to bat. How do we base our estimates on performance? Is past performance an indicator of future performance? Is aging (the player's or the bat's) a factor ? Should we calculate a batting average over the last ten games or over the last ten years? Should we take into account where the games are played and under what weather or field conditions? Should we compare the player's average to the team average? Should we just use an individual performance in computing the average, or should we include the performance of other team members as well (to create a Stein estimator)?
Note that similar problems occur when assessing performance of investments or advisors except that the warning is more explicit (as seen in the oft-repeated phrase in the advertising copy for mutual funds, "Past performance cannot guarantee future results.")
Of course, the risk in not using a quantitative model (and relying on judgement alone) exposes another aspect of model risk: these are errors in judgement are due to anchoring, inconsistency, selectivity, fallacy, and representation.
Many of these problems associated with model risk are discussed in detail in
Models ultimately have to be implemented as a software component or system. The act of implementing a model induces operational risk.
Different implementations of the same model may also perform differently or react differently to different adverse events, or may simply stop working at a particular moment in time. A famous example of this type of operational risk is the current "Y2K" problem associated with an implementation of the calendar: some implementations represented a year between 1900 and 1999 by the last two digits. What happened to systems that relied on these implementations in the year 2000?
What is even worse, a model or the underlying implementation may not even be testable: a testable model or implementation should be observable and controllable: it should not exhibit any test input-output inconsistencies. Here, observability refers to the ease of determining if specified inputs affect the outputs; controllability refers to the ease of producing a specified output from a specified input. A model or implementation that is not easily testable may cause several problems, as discussed in
On the other hand, other implementations may just simply "blow up." Thomas Edison was an eye-witness of a few operational disasters on Wall Street (including the "Black Friday" of 1869):
In those days, the chemical batteries — used to generate electricity to power the telegraphs — would frequently explode. Power failures are still a concern on Wall Street.
Finally, even if all these are implemented correctly there may be legal or compliance risk due to obligations to regulatory bodies. Regulatory organizations try to guarantee safety or prevent illegal activities. For example, in the U.S., some regulatory governmental agencies include:
- Occupational Safety and Health Administration
- Department of Transportation
- Environmental Protection Agency
- Federal Trade Commission
- Securities Exchange Commission
- NASD Regulation
Not being in compliance with rules can be costly. Some activities can put a firm at risk for being fined or for being put out of business.
The specific problem here is to assess the value of a security or portfolio of securities given an adverse event: an assessment of "When bad things happen to good portfolios." For example, recent sudden changes in credit and interest rates (which may or may not be due to economic, political, or emotional factors) have had devastating effects on some security prices and ultimately on the financial health of some portfolios (and some investment firms).
Some quantitative models of securities are based on factors that can be directly observed from "the market" (such as security prices, interest rates, or currency exchange rates) — at any time the security is traded or when a price is quoted. Other models are based on factors that can not be directly observed from the market (such as credit ratings, inflation indicators, or monetary indices).
Some non-market factors are made available through periodically published government or agency reports, for example, through the Federal Reserve's FRED database. Other factors, such as credit ratings, are provided by vendors (such as Standard & Poor's) or by proprietary research.
Aspects of model risk that are specific to financial models are discussed in
Traditionally, market and non-market factors are modeled as separate components and integrated later.
Market Risk: A Simple Model of Returns
One model of security prices assumes that the security returns over a given time period are reasonably constant. A formula for the daily return on a security is
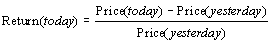
A savings bank account is an example of an riskless investment that provides a constant return. For example, if a savings account pays 3% per year, if we deposit $100 today, we will get $103 in one year (=100+3%*100).
A formula that expresses this relationship is
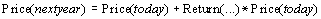
This relationship can also be seen in the following charts:
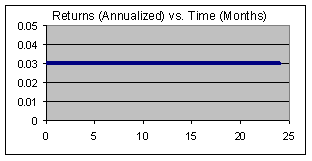
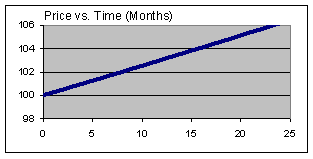
These charts graph the simple return of a security (set at a 3% annual return) and its corresponding price over the next 24 months. Note that the appealing aspect of a savings account is that returns and price are predictable by contractual commitment and that returns compound.
For example, the value in 2 years is the value after the first year plus the return on that amount after one year, or
- Price(end of 2 years) = [ Price(end of 1year) ]+
3%*[Price(end of 1 year)]
- Price(end of 2 years) =[100 + 3%*100] + 3%*[100 + 3%*100] = $106.09.
This complicated expression can be factored to 100*(1+3%)*(1+3%). Note that compounding includes the return on the return.
There are other methods of reckoning returns that depend on the bank account or contractual arrangement. Returns depend on the frequency of compounding (e.g., the return can be compounded annually as above, or can be compounded quarterly, monthly, or daily, hourly, or even continuously). There are returns that depend on how one represents the number of days in a year (e.g., usually 365 days, but what if the year is a leap year? If we assume all months have 30 days then we get a 360-day year. ). The good news is that there are conversion formulas that represent one of these returns in terms of other returns — just like the formulas for converting meters to inches. When evaluating the returns of bank accounts or other contracts, we need to have to have a common return language.
So far the model does not include risk. Returns and market prices for a risky security (like a stock) have sudden increases and decreases and look something like this:
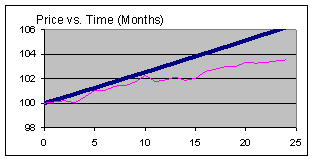
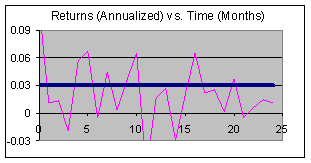
Note that the returns can even be negative (which can lead to a loss instead of a profit). Risky returns and market prices exhibit "noise." (One reason for such "noise" is that prices depend on free and open markets and these markets depend on people with conflicting goals, requirements, and emotions. All of these factors are integrated by what Adam Smith called "the invisible hand" to form a price.) These two charts superimpose the noisy return (and price) paths over the riskless paths: they show on retrospect, the returns and prices of a risky security over the last 24 months.
Can we predict future returns and prices with certainty? If we know how returns and market prices evolve then we may be able to determine likely values of returns and prices. One simple model assumes that the returns over a short time period follow the bell-shaped normal probability distribution. For example, we can assume that daily returns cluster around a mean or average: on some occasions there are good days (higher than the average daily return) and bad days (lower than the average daily return). Note that the normal bell-curve is symmetrical around its mean.
The thickness of the bell-shaped curve (a measure of the average distance from the mean) is another parameter called the standard deviation. The standard deviation is frequently used as a proxy for volatility: the impact of sudden price changes due to unusual events.
These two parameters of the normal distribution determine the likelihood of very bad days and very good days. Consequently, if we know the parameters, then we can assess the likelihood of any price path in time from an infinite number of potential price paths.
The following chart shows several potential price paths of a security having a mean daily return of 0.0125% (which is equivalent to a monthly return of 0.25% and an annual return of 3% a year). In some ways, it shows how prices can evolve in several parallel universes:
The simple model assumes that the mean and standard deviation of daily returns are constant in a short time period: this implies that these parameters can be estimated from an historical time series of market prices or returns.
Once we have estimated these statistical parameters, we can compute a histogram of prices over a given time horizon: a frequency chart that shows a range of prices together with the percent of time that the price will be in that range. The histogram corresponds to a vertical time slice through the above chart of potential price paths.
For example, this histogram shows the potential values of a
security over the next 10 days, together with the probability of the
values. It looks like a normal bell-curve, symmetric around its mean
value (approximately 55). The histogram shows that the value of the
security will be between 53.93 and 56.61 approximately 80% of the
time: The chart also shows that the value of the security will be
less 53.93 approximately 10% of the time in the next 10 days. So if
the price today was actually 55, then there is a 10% chance that, in
the next 10 days, we will lose 55-53.93 = 1.07 — or almost 2%
(1.07/55) — of the original value of the security. Questions like assess what is called the Value
at Risk
(VaR): the VaR of a security depends on a time
horizon and a probability of an adverse event occurring at the end
of that horizon. Note that if the returns of the security are
normally distributed, then we can derive a formula for VaR. If s
denotes the (constant) daily standard deviation of the returns, and
m denotes the (constant) mean return, and if the price of a security
today is P, then the VaR for an adverse event with 5% probability
over the next T-days is approximately (Note that if the model assumes that the mean daily return m
is zero, then we have the model and formula used by the J.P. Morgan
RiskMetrics group.)
One reason for computing VaR is to establish cash reserves in
case the security has to be sold at a loss. For example, the Bank of
International settlement recommends that a bank should have at least
three times its total 10-dayVaR (based on a 1% adverse event
probability, or 2.33 standard deviations) as a cash reserve to
protect itself against adverse situations.
Another reason for computing
VaR is to assess how much insurance would be needed to cover
potential losses. The rationale for the multiplication factor of three is
because of model risk — we observe that adverse events happen
more often than predicted by a normal distribution. For most
securities, the observed probability distribution of returns has
"fatter tails" than a normal distribution. The factor of
three effectively stretches the observed tail out to 7 standard
deviations. (According to a famous result in probability theory
known as Chebychev's Inequality, 7 standard deviations is actually
enough to specify a 1% adverse event probability for any probability distribution symmetrical around its
mean.)
A Simple Model of Portfolio Returns: Portfolio
Trigonometry
For portfolios of more than one security, the standard
deviation of a portfolio is not necessarily the sum of the standard
deviations of the securities in the portfolio. If we still assume
that the returns of the securities in the portfolio follow the
simple model (all returns are normally distributed with constant
standard deviation) then the return on the portfolio is a normal
distribution in several dimensions — one dimension for each
security — called a multivariate normal distribution. In this
case, there are a set of statistical parameters that become a proxy
for volatility (in addition to the individual security standard
deviations), such as the covariances, and correlations.
The important effect in a portfolio is due to correlation: the
statistical version of the idea "Don't put all your eggs in one
basket." We can understand the effect of correlation even on a
portfolio of only two securities.
Note that two securities are dependent in some time period if
they consistently move in the same way (positive correlation) or if
they consistently move in opposite ways (negative correlation).
For example, in
a particular time period, various treasury securities are positively
correlated with each other because when one treasury rises in price
they all consistently rise in price; the same treasuries may be
negatively correlated with stocks because over the same period when
treasuries rise, stocks fall. Here is an example: Astra Pharmaceuticals has symbol A, Barnes
Group has symbol B. Let's construct a portfolio made up of $100 each
of A and B. What is the standard deviation of the return of the
portfolio? Combining standard deviations of two securities is like
combining the third side of a triangle from two given sides. For
example, suppose s(A) and s(B) denote the standard deviations of the
returns of A and B: Note that in the above diagram, stock A has a larger standard
deviation than stock B. It turns out that the standard deviation of
the portfolio returns, denoted by s(A+B), is the magnitude of the
third side of a triangle formed by s(A) and s(B). Note that for any triangle, the sum of any two sides must be
greater or equal to the third side. The missing detail that allows
us to draw the triangle — the angle between s(A) and s(B)
— is related to the correlation between the returns of A and
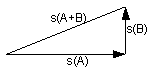
B. Depending on the angle between them, the triangle can be
either an obtuse triangle (positive correlation) —
— or an acute triangle (negative correlation) —
or a right triangle (zero correlation) —
Computing portfolio standard deviation becomes a problem in
trigonometry. For more than two securities, the correlation is
measured by representing all the combinations of angles between all
the individual security standard deviations.
The actual
measure of positive or (negative correlation) is given by a
statistical formula called the correlation coefficient: it is a
number between -1 and +1 that is related to the angle between s(A)
and s(B). [The correlation coefficient is actually the negative cosine of the angle between s(A)
and s(B).] So, according to portfolio trigonometry, for zero or
negatively correlated securities, the standard deviation of the
portfolio is always less than the sum of the standard deviations of
the individual portfolio components: risk is reduced by diversifying
into non-correlated asset classes. (Note that the portfolio standard
deviation can even be zero if two securities have the same standard
deviation and have perfect negative correlation.) This risk management diversification technique is used
extensively. One application is discussed in
Of course, the big problem is assuming that correlations do
not change in time (in the real world they do). Finding the right proportional mix of securities — the
one that maximize the portfolio return and minimizes the portfolio
standard deviation (the proxy for risk) is a problem in
optimization. If one puts additional constraints on the problem (for
example, limiting the proportion of each security or prohibiting
short selling) then the optimization techniques become a little
involved. Different implementation of such portfolio optimization
techniques is discussed in
Insurance, Hedging, and Replicating
Portfolios
How much does an insurance policy cost for replacing a
security over a given time period? The cost of insuring an asset
depends on its current price and the value of the insurance
"deductible" (also known as the strike price). It also
depends on the probability distribution of the value of the asset
and the current interest rate. If the returns of a security are normally distributed with
zero mean, then it turns out that the 10-day VaR is equal to the cost of a 1-year
zero-deductible insurance policy, guaranteeing the policy holders
full replacement of the original price of the security in cash.
In the market, this insurance takes the form of a put option
— a contract that protects against price losses in the
security over a certain time horizon (the maturity) and below a
specified price barrier (the strike price). A put option gives the
holder the right to sell a security at a specified strike price at a
specified time. If the returns of a security are normally distributed with
constant standard deviation, and if the current short-term interest
rate is constant, a formula (the famous Black-Scholes
formula) exists for pricing a put option
and a call option. (A call option
gives the holder the right to buy a security at a specified strike
price at a specified time.)
Options can have other contractual conditions. They are an
example of derivative securities
— their value (an insurance cost) is derived from the
value of an underlying security. In
general, computing the value of a derivative security is a difficult
problem in mathematical finance, especially for more complex models
and contracts. For a discussion of the computational tradeoffs
involved, see: Suppose the underlying security suffers an adverse change.
What would then be the new price of an insurance policy (a put
option)? A similar question is: Suppose the price of a security depends on some underlying
factor, like the interest rate. Suppose we also know how the price
of the security changes when the interest rate changes. This ratio
of price change to rate change is actually the slope of a line (also
called the Delta) as the following figure shows:
Given an initial price and slope, we can draw a line that
approximates (or predicts) the price movement based on any given
interest rate movement. We can extrapolate the line to cover any change in the
underlying factor. Note that this extrapolation is only a linear
approximation of what may be the actual price: the error in the
approximation increases for large changes in the underlying interest
rate. Conversely, the error in the approximation goes to zero as the
changes in the underlying interest rate decrease to zero.
The ratio
of infinitesimal price changes to infinitesimal rate changes —
which approaches the slope of a tangent line at a given price
— is called the first derivative. It is the instantaneous rate
of change of the price with respect to the underlying factor. Note
that the use of the word derivative (from differential calculus), is
different from its typical use in finance relating to derivative
securities. To avoid confusion, we call the first derivative by names like
Delta and Vega.
We can make a better approximation if we create another curve
— by plotting different slopes over the price curve —
and then look at the slope of that curve. This slope of slopes (the
Delta of a Delta) is called the second derivative.
To avoid confusion, we call
the second derivative by names like Gamma.
Consequently, if we can compute these Deltas and
Gammas then we
can compute a reasonable approximation to the new price given a
change in the underlying factor. Note that this result is
non-parametric — it does not assume that the underlying factor
or the price follows a normal distribution (or any distribution).
We can use the Black-Scholes
formula for the price of an option to derive formulas for the
Deltas and Gammas, relating the change in price of an option with
respect to changes in its underlying. The formulas are valid as long
as the returns of the underlying security are normally distributed,
the returns have constant standard deviation, and the current
short-term interest rate is constant.
The Deltas and Gammas are sensitivity coefficients that relate
changes in underlying factors to changes in a security. They are
sometimes called hedge ratios since they can be used to provide
another type of insurance. Note that if two securities have the same
Deltas and Gammas then they react similarly to similar changes in
the underlying. So to replicate the behavior of one security (or
portfolio of securities), we need to match the Deltas and Gammas in
the other security (or portfolio). In general, the problem of
constructing a replicating portfolio
that mimics the behavior of a given security is reduced to
finding the right linear combination of hedge ratios — a
problem in algebra.
Credit risk is concerned with to the cost of replacing an
asset or contract if a party defaults on the arrangement. It could
be assessed by a potential decrease in credit quality: the ability
to repay obligations. Market risk is the potential loss that is
associated with a market price movement. If the price movement is
specified by a given probability over a specified time horizon,
then, as we saw above, market risk represented as value-at-risk (VAR). Credit quality is an attribute of a firm that is difficult to
observe directly from market prices. Credit quality is assessed by
different rating agencies using both a qualitative and quantitative
methods. They then group credit-similar firms or parties into
different credit classes or ratings. The most credit-risky class is
the default class. Different agencies typically assign a
"letter grade" to each class.
An example of the different factors involved in a credit
quality assessment is in From a quantitative perspective, credit risk assessment can be
measured if we can estimate or predict the probability distributions
of the likelihood of default (the default
probability) and the percentage of the asset that creditors can
recover in the event of default (the recovery rate).
Different ratings agencies create a transition probability
matrix: a table that lists the probability of going from one credit
class to another over a given time period (for example, in one
year). For example, the following table provides the one-year
transition probabilities for a set of credit classes:
So for example: If these transition probabilities do not change from one
period to the next, then a transition probability across multiple
periods can be computed. (This is called the stationary Markov
assumption.) Consequently, the default probability can be computed
for any time period given the knowledge of the transition matrix
(using a procedure called matrix multiplication). Consequently, the
2-year transition probabilities are:
Now, Note how the transition probabilities "migrate" to
lower probabilities: if we wait long enough, all risky firms will
eventually have higher and higher probability of default.
Credit agencies also tabulate recovery rates for credit
classes: the likely proportion of the security that a holder could
recover in the case of default. Recovery rates are between 0%
(recover nothing) to 100% (recover everything). All of these are
statistically estimated — but not directly from market prices.
One illustration of the impact of credit risk was seen in
September 1998, when the Long Term Capital investment fund was rescued by a $3.6 billion private bailout by a group of
banks and brokerage firms with the coordination of the Federal
Reserve. (The reason for the bailout was that Long Term Capital
borrowed some of its money from its investors in the form of
unsecured loans. If Long Term Capital defaulted, the investors also
could have defaulted and trigger a chain reaction of further
defaults.) One trading strategy that Long Term Capital used was a credit
spread: U.S. Treasury bond futures are sold short (assuming they
could be bought back at a lower prices), and higher yield (and
higher risk) bonds are bought with the proceeds. The strategy makes
money as long as Treasury bond prices remain stable or fall. (This
strategy is similar to the TED spread strategy discussed in
Confronting Uncertainty:
Intelligent Risk Management with Futures.) Another strategy Long
Term Capital used was to invest in Russian bonds, with the
assumption that United States, the International Monetary Fund and
The World Bank would immediately rescue Russia from any potential
default: thus rendering the default probability of Russian bonds
close to zero.
The first strategy blew up when the stock market began falling
in July: bond prices rose as investors chose to buy securities
backed by the U.S. government (the "flight to quality and
safety"). The second strategy blew up when Russia actually
defaulted.
The simplest model for security prices assume that its returns
are normally distributed in a specific time period (with constant
standard deviation), and that the short-term interest rate is
constant. There are several problems with this model that are observed
in practice. First of all, none of the parameters are constant: means and
standard deviation change in time. This implies that the models need
to be continuously recalibrated. A more serious problem is that interest rates are not
constant. This problem is especially critical for interest rate
sensitive securities such as bonds. A bond is a security where the owner receives a fixed
unconditional promise (from someone) to pay a specific principal
amount of cash at a specific future date (the date when the bond
matures). Unlike a stock, the price of a bond is known at some fixed
future time. (The market determines the price of a bond at all other
times. The market determines the price of a stock at all times
— present and future.) Bonds may also pay intermediate
payments (coupons or interest payments) at other times. Bonds can
have other contractual conditions on the principal, interest and
payment dates. For example, floating-rate bonds have variable
coupons (whose value depends on an interest rate); mortgage-backed
bonds have variable principal or coupons (whose value can change due
to mortgage pre-payments). Note that a bond price does not behave like a stock price: the
price of a stock can range from zero to any large value (even as
high as $76,600: the May 10, 1999 price of one Berkshire Hathaway
class A share). A bond price is usually less than its known price at
maturity: it cannot grow to any arbitrary value.
After a bond is issued, its price may fluctuate; just before
it matures, its price converges to its promised payoff. This implies
that the standard deviation of bond returns increases (when it is
issued), fluctuates during its life, and decreases to zero at
maturity. (This is known as the pull-to-par effect.)
Bond prices depend on an interest rate: the problem is which
interest rate? Very simply, for a bond that does not pay any coupons
(a zero-coupon bond) that matures in exactly one year, its simple
annual interest rate (or "yield") is just its return:
There is an implicit interest rate for every bond issued by a
government, corporation or individual. Like returns, there are
formulas for interest rates that depend on the frequency of
compounding (e.g., a simple interest rate compounded quarterly,
monthly, annually or continuously).
There are rates that depend on how one represents the number
of days in a year (e.g., the "discount" rates for 90-day
U.S. treasury securities assume a 360-day year). The good news is
that there are formulas that represent one of these rates in terms
of other rates: we just have to agree on a common interest rate
language. For longer time periods, the rate is its compounded return.
For example,
suppose the principal of a 5-year zero-coupon bond is $100. The
formula linking today's price with its (annual) spot interest rate
is: This shows that the price of a bond can be given by its spot
rate and vice versa. Here is another example. Suppose a 1-year
treasury security promises to pay $100 in exactly one year. Today it
sells for $90. Then the 1-year interest rate —called the
1-year spot rate —is then given by (100/90)-1 =11.1111% (to
four decimal places). Note that the value of $90 one year from now is
$90*(1+11.1111%) = $100.
If a 2-year treasury security promises to pay $100 in exactly
two years sells for $80 today, then its 2-year spot rate is then
given by
Note that because of compounding, the value of $80 two years
from now is $80*(1+11.8034%)*(1+11.8034%) = $100.
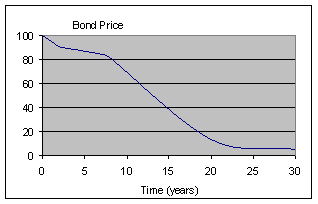
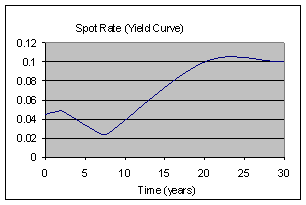
Given the appropriate bond price, we can similarly compute
2-year, 5-year, 30-year spot rates, as well as 6-month, 3-month, and
1-day spot rates. The combination of all (zero-coupon) bond prices from an
issuer create a yield curve; here is an example that shows the
correspondence between yield curves of bond prices and spot interest
rates:
Another interest rate is the forward rate. The forward rate is
often a proxy for an unknown future spot interest rate.
Here is an example. Suppose today is January 1, 2000, and that
today's prices and rates of 1-year and 2-year zero coupon bonds are
as calculated as above (the 1-year bond is $90 or 11.1111% and
2-year bond is $80 or 11.8034%). Suppose we need to borrow $100 on
January 1, 2001 (in a year from now), and we will pay the money back
a year after the loan is made on January 1, 2002 (which is two years
from today). Given these facts, what would be the interest rate at
the time of borrowing? We really need to know the one-year spot rate on January 1,
2001. But we only know the 1-year spot rate today (which is
11.1111%); we do not know the 1-year spot rate in the future.
However, we can compute an "implied" future 1-year spot
rate, given the value of today's 1-year and 2-year spot rate. This
1-year forward rate from 2001 to 2002 is the rate of return from
2001 to 2002 such that, the when it is compounded with the rate from
2000 to 2001, the resultant return is the spot rate from 2000 to
2002. In other words, it is the unknown value in the following
expression: In this case the forward rate is 12.5%. The forward rate can also be computed directly from the bond
prices: Some people believe that forward rates are predictors of
future spot rates, just as they believe that forward prices of an
asset or commodity are predictors of future spot prices. In general
they are not. Forward rates simply correspond to the implied
interest rates of bond futures: a
contract that delivers a bond in a given time. We still didn't answer the question as to what is the interest
rate. The prices of all bonds issued in the U.S. are correlated to
the prices of U.S. Treasuries securities: bonds backed by the credit
of the U.S. government. Everyone agrees that in the U.S., these
bonds are risk-free. Consequently, risk-free U.S. interest rates are
determined by U.S. treasury securities. Other bonds have lower
prices since they have higher risk (assuming there are no tax
consequences), and their interest rates are higher (and are given by
a spread over a corresponding treasury security).
Consequently, if we have a model for the U.S. risk free
interest rate and a model for the credit spread, then we can
theoretically price any bond in the U.S. This applies to other
sovereign states as well: for example, if we have a model for the
U.K. risk free interest rate and a model for the foreign exchange
rate (that changes $dollars to £pounds), then we can
theoretically price any U.K. bond in U.S. dollars. The trick is in
developing the right interest rate model. Historically, interest rates are rarely less than zero and
never seem to grow unbounded. In ancient Babylonia, interest rates
were unregulated; simple annual interest rates fluctuated between 5%
to 20%. In Rome, one of the oldest interest rate regulations (450
B.C.E) fixed the interest rate to 1% per month (one thousand years
later new regulations actually forbade compound interest in what
remained of the Roman Empire). In more recent times interest rates have been negative for
brief periods (for example, in 1932 in the U.S. and in November 1998
in Japan). Some interest rate models assume that spot rates do not wander
from a long-term drift or mean-reverting rate. Other models are
based on forward interest rates. Most are based on generalizations
of the Black-Scholes model of stock returns, and are expressed in
the language of stochastic differential equations. The following Technical Note provides a brief taxonomy of some interest rate models,
together with a discussion of some statistical techniques used to
derive the model parameters. Integrated
Financial Risk Assessment
We introduced the section on Financial Risk Assessment with the phrase
"When bad things happen to good portfolios." Here we
conclude with some caveats, especially considering that "worse
things can happen to a financial firm," when adverse events
turn into terminal events.
Traditionally, market and non-market factors are modeled as
separate components and integrated later. Market factors include
those factors observable in a market, such as prices and rates.
Non-market factors are not directly observable in the market, such
as credit quality or compliance with regulatory procedures.
Note that some of these factors may be difficult to quantify.
It may be possible to smoothly integrate a few important component
risk factors. See for example, the brief Technical Note and a description of the Inductive Solutions
Risk Kit system.
However, in order to integrate all component risk factors in a
testable way, all factors must be observable and controllable.
Otherwise, it may be difficult to decide exactly where there is a
problem. Moreover, because of correlations between risks, the
integration of risks may be much more than the sum of its component
parts. For example: [At the time, Barings was in the process of installing a risk
management system in its Far East offices. The system was supposed
to alert management to unusual company trading positions. According
to Computing, (2 March 1995): "...Barings' assistant IT
director, was unavailable for comment, but sources believe the
bank's existing settlement system contributed to the collapse. The
Cash Risk Management system was supposed to flag cash positions, but
if settlements were not processed according to the bank's
procedures, it could not do so. "] [Askin Capital invested in mortgage-backed securities —
bonds based on home mortgages that have a low default risk (since
the payments are guaranteed by various federal government agencies).
However, these bonds have prepayment risk: early repayment of
mortgage principal induces an opportunity cost for the investor who
is on the receiving end of the mortgage cash flows. The fund blew up
in 1994, after the Federal Reserve unexpectedly raised interest
rates — for the first time in five years. This sudden increase
reduced the number of homeowners seeking to refinance their
mortgages with new loans. This was completely counter to the
prepayment assumptions made: the value of certain mortgage
derivatives fell. In March 1996, the investors sued three Wall
Street brokerage firms and Askin Capital Management for $700
million.]
Sometimes a firm can we doing very well financially, but may
still be at risk of substantial losses. Some activities can put a
firm at risk for being fined or put out of business: not being in
compliance with rules can be costly. Who sets the rules? In the
U.S., the Securities Exchange Commission is the U.S. agency that
monitors the U.S. exchanges and markets to make sure that they are
fair and orderly and in compliance with the law. Some examples of
high-compliance-risk activities that the SEC monitors are listed in
the How these high-risk activities play out (usually not for the
benefit of the firm) and how compliance systems can be designed to
detect them is discussed in For example, In these two cases, the firms were at risk due to their lack
of compliance with SEC rules and regulations. An integrated
financial risk assessment must take into consideration as many risk
factors as possible as well as the established rules and procedures
of regulatory organizations. Many of these are listed at Many risk factors listed above are difficult to quantify and
observe. On the other hand, even if we have models of these risk
factors, a model that integrates them would also carry its own share
of model
risk. from Robert Burns (1759-1796),
To A Mouse
Philip Davis, SIAM News, October 1994, page 6. Blaise Pascal (1623-1662),
Penseés, no. 173.
Blaise Pascal (1623-1662),
Penseés, no. 233.
Alan Greenspan, New York Times, March 6, 1995. Dick Teresi, Wall Street Journal, January 10,
2001.
(c) 2001
Inductive Solutions, Inc. All rights
reserved.
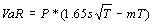
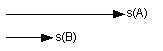
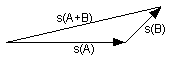
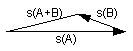
What is the new price of a security given a
change in some underlying factor?
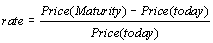
![]()

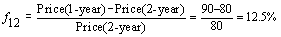
Risk Watch was set up by the International
Finance and Commodities Institute (IFCI) — a non-profit
foundation created in 1984 on the initiative of the Swiss
Futures & Options Association, with the objective of
promoting global understanding of commodity trading as well as
financial futures and options. Risk Watch provides an
introduction, glossary, and guide to the most important official
documents in the area of financial risk management.
GARP is a not-for-profit, independent organization of
financial risk management practitioners and researchers. GARP's
mission is to serve its members by facilitating the exchange of
information, developing educational programs, and promoting
standards in the area of financial risk management